VGGNet是牛津大学计算机视觉组(Visual Geometry Group)和谷歌 DeepMind 一起研究出来的深度卷积神经网络,因而冠名为 VGG。VGG是一种被广泛使用的卷积|神经网络结构,其在在2014年的 ImageNet 大规模视觉识别挑战(ILSVRC —2014)中获得了亚军,不是VGG不够强,而是对手太强,因为当年获得冠军的是GoogLeNet。
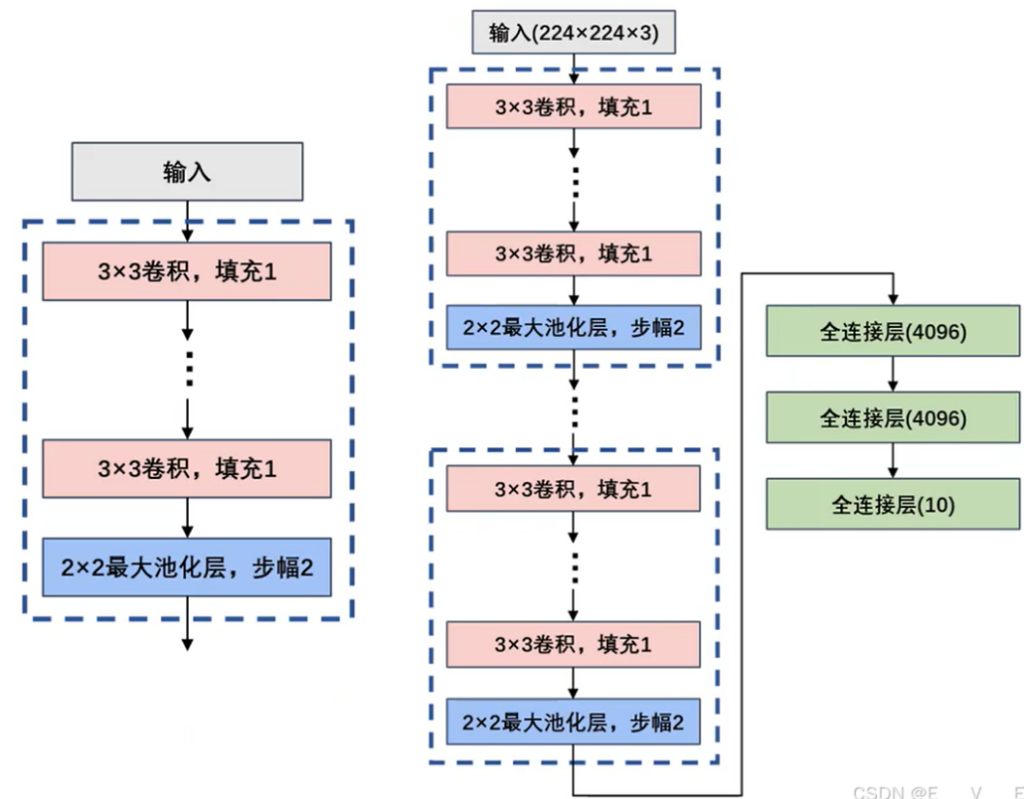
通常人们说的VGG是指VGG—16(13层卷积层+3层全连接层)。虽然其屈居亚军,但是由于其规律的设计、简洁可堆叠的卷积块,且在其他数据集上都有着很好的表现从而被人们广泛使用,从这点上还是超过了GoogLeNet。VGG和之前的AlexNet相比,深度更深,参数更多(1.38亿),效果和可移植性更好。
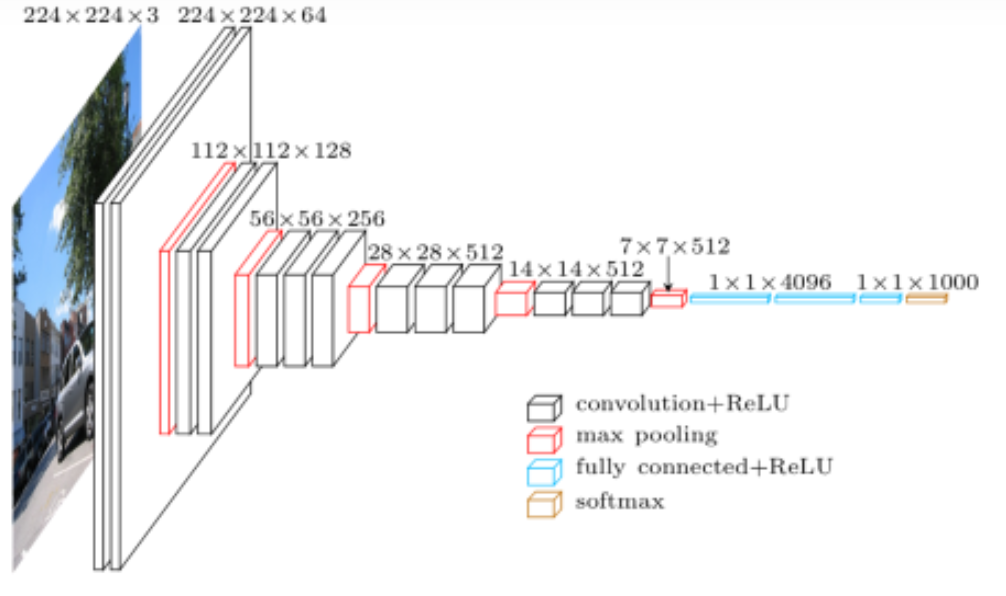
VGG网络结构

卷积就是我们的一个特征图啊往往都会缩小 ,然后的话但它通道不会变.卷积一般是使用我们的通道C变大,磁化但是它的通道就是我们那个H和W一般都会变小.下采样的意思就是使分辨率变小
- vgg—block内的卷积层都是同结构的意味着输入和输出的尺寸一样,且卷积层可以堆叠复用,其中的实现是通过统一的size为3×3的kernel size + stride1 + padding1实现。
- maxpool层将前一层(vgg—block层)的特征缩减一半 使得尺寸缩减的很规整,从224—112—56—28—14—7。其中是通过pool size2 + stride2实现。
- 深度较深,参数量够大·较深的网络层数使得训练得到的模型分类效果优秀,但是较大的参数对训练和模型保存提出了更大的资源要求。(因为到后面的RESNET的时候,你会发现它解决就是我们模型较深,使我们使我们的效果不好的问题)
- 较小的filter size/kernel size **这里全局的kernel size都 为3×3,相比以前的网络模型来说,尺寸足够小。
- 你会发现我们的选集都是3×3,3×3有什么好处呢,参数少对吧防止过滤
参数详解
第1个vgg block层:
(1)输入为224×224×3,卷积核数量为64个;卷积核的尺寸大小为3×3×3;步幅为1(stride=1),填充为1(padding=1);卷积后得到shape为 224×224×64的特征图输出。
(2)输入为224×224×64,卷积核数量为64个;卷积核的尺寸大小为3×3×64步幅为1(stride=1)填充为1(padding=1);卷积后得到shape为 224×224×64的特征图输出。
(3)输入为224×224×64,池化核为2×2,步幅为2(stride=2)后得到尺寸为112×112×64的池化层的特征图输出。
第2个vgg block层:
(1)输入为112x112x64,卷积核数量为128个;卷积核的尺寸大小为3x3x64;步幅为1 (stride =1),填充为1(padding二1);卷积后得到shape为112x112x128的特征图输出。
(2)输入为112x112x128,卷积核数量为128个;卷积核的尺寸大小为3x3x128;步幅为1 (stride =1),填充为1(padding=l);卷积后得到shape为112x112x128的特征图输出。
(3)输入为112x112x128,池化核为2x2,步幅为2 (stride = 2)后得到尺寸为56x5后128的池化层的特征图输出
第3个vgg block层:
(1)输入为56x56x128,卷积核数量为256个;卷积核的尺寸大小为3x3x128;步幅为1 (stride=1).填充为 1 (padding=l);卷积后得到shape为56x56x256的特征图输出。
(2)输入为56x56x256,卷积核数量为256个;卷积核的尺寸大小为3x3x256;步幅为1 (stride=1),填充为 1 (padding=l);卷积后得到shape为56x56x256的特征图输出。
(3)输入为56x56x256,卷积核数量为256个;卷积核的尺寸大小为3x3x256;步幅为1 (stride = 1),填充为 1 (padding=l);卷积后得到shape为56x56x256的特征图输出。
(4)输入为56x56x256,池化核为2x2,步幅为2(stride=2)后得到尺寸为28x28x256的池化层的特征图输出。
第4个vgg block层:
(1)输入为28x28x256,卷积核数量为512个;卷积核的尺寸大小为3x3x256;步幅为1 (stride = 1),填充为1(padding=1);卷积后得到shape为28x28x512的特征图输出。
(2)输入为28x28x512,卷积核数量为512个;卷积核的尺寸大小为3x3x512;步幅为1 (stride=1),填充为1 (padding=l);卷积后得到sh叩e为28x28x512的特征图输出。
(3)输入为28x28x512,卷积核数量为512个;卷积核的尺寸大小为3x3x512;步幅为1 (stride = 1).填充为1 (padding=l);卷积后得到shape为28x28x512的特征图输出。
( 4 ) 输入为28x28x512,池化核为2x2,步幅为2(stride=2)后得到尺寸为14x14x512的池化层的特征图输出
第5个vgg block层:
(1)输入为14x14x512,卷积核数量为512个;卷积核的尺寸大小为3x3x512;步幅为 1 (stride = 1),填充为1(padding=l);忠积后得到shape为14x14*512的特征图输出。
(2)输入为14x14x512,卷积核数量为512个;卷积核的尺寸大小为3x3x512;步幅为 1 (stride 二 1),填充为1(padding二 1);套积后得到shape为14x14x512的特征图输出。
(3)输入为14x14x512,卷积核数量为512个;卷积核的尺寸大小为3x3x512;步幅为 1 (stride 二 1),填充为 1(padding=l);卷积后得到shape为14x14x512的特征图输出。
(4)输入为14x14x512,池化核为2x2,步幅为2 (stride二2)后得到尺寸为7x7x512的池化层的特征图输出。该层后面还隐藏了flatten操作,通过展平得到7x7x512=25088个参数后与之后的全连接层相连。
第1~3层全连接层:第1〜3层神经元个数分别为4096, 4096,1000,其中前两层在使用relu后还使用了Dropout对神经元随机失活,最后一层全连接层用softmax输出1000个分类。
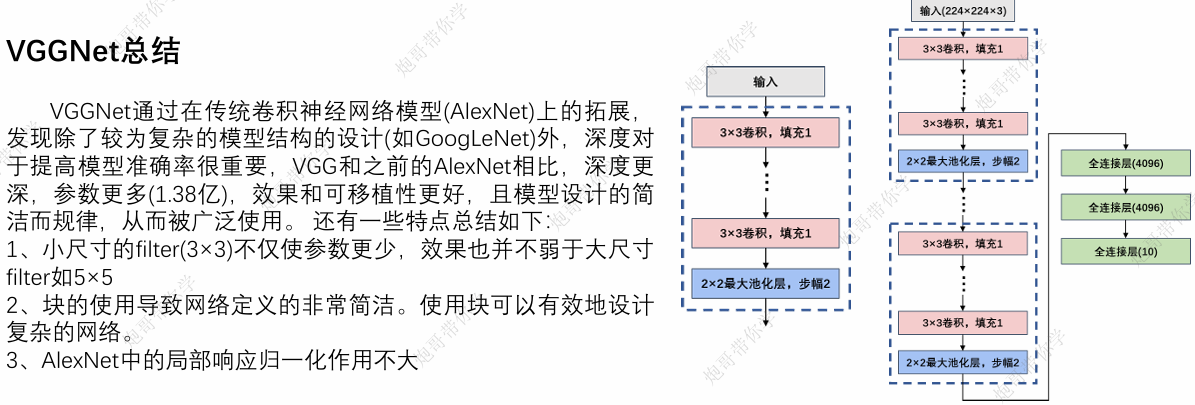
VGGNet通过在传统卷积神经网络模型(AlexNet)上的拓展,发现除了较为复杂的模型结构的设计(如GoogLeNet)外,深度对于提高模型准确率很重要,VGG和之前的AlexNet相比,深度更深,参数更多(1.38亿),效果和可移植性更好,且模型设计的简洁而规律,从而被广泛使用。还有一些特点总结如下:
1、小尺寸的filter(3×3)不仅使参数更少,效果也并不弱于大尺寸filter如5×5
2、块的使用导致网络定义的非常简洁。使用块可以有效地设计复杂的网络。
3、AlexNet中的局部响应归一化作用不大
VGG代码实战
model.py
import torch
from torch import nn
from torchsummary import summary
class VGG16(nn.Module()):
def __init__(self):
super(VGG16, self).__init__()
self.block1 = nn.Sequential(
nn.Conv2d(in_channels=1, out_channels=64, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=64, out_channels=64, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.block2 = nn.Sequential(
nn.Conv2d(in_channels=64, out_channels=128, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=128, out_channels=128, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
)
self.block3 = nn.Sequential(
nn.Conv2d(in_channels=128, out_channels=256, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=256, out_channels=256, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=256, out_channels=256, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.block4 = nn.Sequential(
nn.Conv2d(in_channels=256, out_channels=512, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.block5 = nn.Sequential(
nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.block6 = nn.Sequential(
nn.FLatten(),
nn.Linear(7 * 7 * 512, 4096),
nn.ReLU(),
nn.Linear(4096, 4096),
nn.ReLU(),
nn.Linear(4096, 10),
)
def forward(self, x):
x = self.block1(x)
x = self.block2(x)
x = self.block3(x)
x = self.block4(x)
x = self.block5(x)
x = self.block6(x)
return x
if __name__ == '__main__':
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = VGG16().to(device)
print(summary(model, (1, 224, 224)))
model_train.py这次训练的结果不是会很好,暴露问题,使用1060训练了332min即5.5个小时
接下来我们来看一下模型的一个训练的一个结果啊,呃前面也讲了,这次的训练的结果呢,它不会很好,我们是用来暴露我们的问题了,然后的话根据我们的问题干嘛啊,就是来解决对应的问题嘛对吧,首先我们来看一下就是整个训练的一个过程啊,训练过程是 332 分钟,也就是将近大概是五个半小时左右嘛对吧,五个半小时左右时间还是很长的啊,20 轮五个半小时还是很长的,然后的话我们这个,你其实我们从这个通过什么打印出来一个训练日志可以发现啊,基本上它的一个什么呃精度都是在 0.9 左右,也就是在什么啊,0.09 左右也就 10%左右嘛是吧,然后它的 loss 值啊,也基本上大概大概在这个值左右吧,基本上是不变的一个过程,而通过我们的图呢也更加直观,他这个精确度呢基本上就在这个附近,然后他那个 loss 值啊也也也不收敛,也就是这两个 loss 值和我们精确度都不收敛,额这里我插插一个,就是题外话,当时我在写这段代码的时候,我肯定也做了一些测试嘛,哎当时会出现什么情况呢,我训练完之后呢,诶他出现这个问题呃,我我我检查一下了模型啊,发现的模型好像是吧,没有什么问题啊是吧,我就很苦恼,后面呢就是干嘛,后面过了几天之后,我同样代码我也没有改,我也很忙嘛,我没有改,然后又运行同样的代码,我发现诶他又运行 OK 了,然后我就一直思考,我到底是不是有人动了我代码,还是我自己就是迷迷糊,不知道,动了代码之后呢,然后运行运行一下代码之后呢,然后呃它就变好了,对不对,就比如我们的精度啊,一直一直上升,可能最后在大概在 90%多的准确度,还是蛮蛮不错的,对不对,然后的话那代码我也没动,过几天我又又又重新训了一下,之后发现又又不行了,然后不断的重复又训又重复不训呃,就重复训,然后每次是吧嗯结果都不一样啊,就是比如说训了五次之后,哎呀它的精度都是这样子的,不收敛是吧啊,过了下午的时候呢,或者关关机重启之后呢,可能过了一会儿他又好了,哎那时候我就不知道是什么样的原因,就很疑惑,我当时怀疑是不是环境的问题,问哪个问题啊,终于在后面啊,我终于知道问题出在哪里啊,这里我给大家讲一下啊,首先啊给大家讲个这个知识点啊,首先我们模型搭建,我这里给大家讲一下,肯定是没有问题的啊,这里我可以给大家保证,这里模型搭建肯定是没有问题的,然后的话啊这里给大家讲这个知识点啊,首先我们这个 VGG 对不对,危机是十六十六个层,对不对,然后的话因为模型啊,它相对于我们前面 NSNET 和 n net,它相对来说比较深,声对不对,那就意味着什么呢,因为你这里输入一个 X 是吧,输入 X,然后这里比如说通过模型,通过模型,通过模型啊,我们打个省略号,通过模型对不对,然后一直到最后的 Y 对啊,这里肯定是没问题的,对不对,然后的话呢嗯对的话,你最好还能得出我们的 loss 值,你通过 loss 值不断的去反馈过来是吧,去更新我们的一个什么 W 的,对不对,然后我们前面也也知道,我们 W 更新应该是什么样子的,应该是这样的,对不对是吧,这里是我们的什么 loss 值的函数,然后对对什么对我们的 W 是一个什么,是求导的过程,事实上你你会发现随着网络越越来越深啊,随着网络越来越深,你其实你很容易出现什么,前面我也讲过,也容易出现什么梯度消失这种问题,就消失或者梯度爆炸,这个问题导致你的 W 更新之后,其实事实上效果不会很好,或者直接就不收敛了,不收敛对不对啊,不收敛啊,直接就不收敛,因为什么呢,因为你这里链式求导嘛,你比如说打个简单,比方你你你你的你的一个 loss 值对什么,对我们的一个你的 loss 是对我们的 W 进行求导,事实上它是这样子的,他可能对 A 函数求导,A 函数又是 B 函数的导数,是吧啊,B 函数可能是 C 函数的导数,C 函数可能是 D 函数的导数,对不对,然后 D 函数,D 函数可能才是 W 的函数的导数,事实上嗯这个还是少的,可能就五层,事实上你想象一下就是五层十层是吧,呃可能十几层他可能就是越来越深了嘛,越来越深的话,你会发现你会发现,就是如果你你你你链式求导的话,你这里导数假设是很小的话,你这里也很小,你这里也很小,你这小这里也很小的话就会导致什么,你这里这个值趋近于零嘛,就问你这里减跟没减它不是一样的吗,你 W 就会不更新,对不对,然后的话然后的话往往往往会出现什么情况呢,就是因为一开始是随机的嘛,应该是随机的,对不对,一开始随机会出现什么过大或过小,过大或过小的这种情况是吧,前面我们在讲我们那个什么原理的时候,再讲深度学习那个呃前面那个基础知识的时候,我们前面也讲了嘛,就是我们前面用一个案例去计算什么,梯度下降法,就是反向传播这样的过程嘛,当时的话我们 W 啊是吧,我们一个初始化的值,比如说等于一,那假设你初始化值可能等于一个过大一个值,你你去比如说你这里啊过大值是吧,事实上真实值最优的值可能是,假设我们 W 初始值是 100 上,最优的值可能是什么,是 0.1,有可能吧,然后的话你这里啊你正常,哪怕你正常更新的情况下是吧,正常更新的情况下,它会导致什么,你最后你其实你更新完之后,你可能再乘个学习率之后,你这里相当于减一个 0.0001,对不对,有这种可能吧,有可能吧,你讲完之后呢,事实上你 0.001 和什么和 99.9999 几乎上没什么区别嘛,但你最优的一个什么 W,应该是在这个区域嘛对吧,所以说最后导致你嘛模型它不收敛,事实上我们希望什么,事实上你其实你的一个码,你随机初始就是你的你 W1 开始随机随机,随机随机什么赋值的时候,你不应该这么这么这么这么这么这么随便,对不对,所以的话就是我们会有什么,会有一个就是随机初始化的一个方法是吧,来来给你们再再再么在训练我们模型之前,我们把我们把我们 W 按照一定的方式是吧,按照一定的方式去初始化,按照一个方法去初始化哎,让他不至于这么离谱吗,明白我意思吧,而且因为 W 会乘上乘上我们对应的 X,它会经过什么,经过我们的激活函数,比如六激活函数啊,或者什么 SM 的激活函数啊,事实上在有时候,这六激活函数或者 single mode 激活函数啊,它在某个区间内它在什么导数是怎么说呢,或者趋向于趋向于零的,对不对是吧,或者比如说我们 LOL 函数,直接就是这样一个分段函数,在这个区间内,在这个区间它是没有没有导数的,对不对是吧,如果你的值所以就落在这里的话,你就不更新了呀,对不对,我们可能希望这个值可能落在这个附近,在某个值的时候它不更新啊,再有的只是它更新,对不对,这样我们希望这样子的吧,如果你这个 W 乘以 X 的值全部落在这个地方,那那你就全部去按零,它直接不更新了呀,那你 W 减去最后减去了 W 等于什么,等于减去一个几乎接近于零的一个数,他就不更新了吗,那最后你等于什么,你的 loss 值,你的 loss 是肯定是不会下降的呀,最后你的精确度也也不会上升的呀,明白我的意思吧,所以其实就是有这样的一个方法来干嘛,来初始化我们的 W 这样子怎么干嘛,就使我们最后的一个更新的速度,第一个可能会变快,第二个什么不至于像刚刚那样不收敛啊,所以的话当时啊就是在写这段代码的时候,我没有加上了,加上一个,这就是我们权重初始化这个这一项导致什么,导致我们模型在训练的时候诶,他好像什么就是一直不收敛是吧,然后的话就又又前面也讲了,那可能过一段时间之后,我再重新运行这段代码的时候是吧,哎可能当时他的因为权重是那个 W 是随机的嘛,W 随机的话可能恰好诶是吧,恰好这一组 WA 比较接近我们真实值,这组 W 比较接近我们的真实真实 W 对不对,哎那可能更新很快就更新好了是吧,所以就会导致什么呢,每一次更新之后是每一次运行,可能过五次运行它不收敛,可能第六次他又收敛了,所以当时就让我很苦恼啊,所以啊所以当我加了什么,加上我们一个什么啊,权重初始化的一个什么方法之后,初始化啊,初始化复制这个方法之后呢,哎基本上你在什么在我们那个运行之后啊,他的一个什么就是结果是很稳定的啊,基本上就是呃大概十轮二轮之后,他就基本收敛了,所以的话接下来我们来看一下,就是既然我们权重是需要初始化的对吧,我们权重是需要初始化的,呃,那我们用代码怎么去,怎么去初始化我们那个权重啊,这里面还讲一下,其实你会发现我们那个 ALICENE 和我们的 net,他当时是没有初始化这个选项的,呃我思考了一下,可能因为这个这个权重啊,这个这个这个模型它不够那么深,所以的话呢可能全都在在在我们什么随机随机,什么随机进行什么啊,进行一个复制之后,然后进行更新,它也是 OK 的,明白我意思吧,事实上在 alex net 我也出现过什么,就是当时没有权重初始化是吧,然后我运气说哎发现他也没收敛,有用这种情况,但基本上我基本上每次运行这个 ANNASNET 的时候,它的效果都是还是 OK 的,正常都会都会训练的,但是呢随着网络越来越深,比如说我们什么 VG 啊,后面讲的 google,后面讲公开的,它都是需要什么权重知识化的,否则很容易出现什么,很容易出现 A 你你你你你你你运行,然后的话可能二轮他都不收敛啊,loss 值也不下降是吧,我们那个精度也不上升这种情况啊,所以的话这一点我们先讲一下,这个就是我们什么权重初始化,怎么在代码当中加上一个权重初始化,这个方法使我们权重啊,更符合我们真实的实际情况啊,好吧,接下来我们来写定义的代码。
VGG16代码
model.py
import torch
from torch import nn
from torchsummary import summary
class VGG16(nn.Module):
def __init__(self):
super(VGG16, self).__init__()
self.block1 = nn.Sequential(
nn.Conv2d(in_channels=1, out_channels=64, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=64, out_channels=64, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.block2 = nn.Sequential(
nn.Conv2d(in_channels=64, out_channels=128, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=128, out_channels=128, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.block3 = nn.Sequential(
nn.Conv2d(in_channels=128, out_channels=256, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=256, out_channels=256, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=256, out_channels=256, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.block4 = nn.Sequential(
nn.Conv2d(in_channels=256, out_channels=512, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.block5 = nn.Sequential(
nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512, out_channels=512, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.block6 = nn.Sequential(
nn.Flatten(),
nn.Linear(7*7*512, 256),
nn.ReLU(),
nn.Linear(256, 128),
nn.ReLU(),
nn.Linear(128, 10),
)
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, nonlinearity='relu')
if m.bias is not None:
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
nn.init.normal_(m.weight, 0, 0.01)
if m.bias is not None:
nn.init.constant_(m.bias, 0)
def forward(self, x):
x = self.block1(x)
x = self.block2(x)
x = self.block3(x)
x = self.block4(x)
x = self.block5(x)
x = self.block6(x)
return x
if __name__=="__main__":
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = VGG16().to(device)
print(summary(model, (1, 224, 224)))model_test.py
import torch
import torch.utils.data as Data
from torchvision import transforms
from torchvision.datasets import FashionMNIST
from model import VGG16
def test_data_process():
test_data = FashionMNIST(root='./data',
train=False,
transform=transforms.Compose([transforms.Resize(size=224), transforms.ToTensor()]),
download=True)
test_dataloader = Data.DataLoader(dataset=test_data,
batch_size=1,
shuffle=True,
num_workers=0)
return test_dataloader
def test_model_process(model, test_dataloader):
# 设定测试所用到的设备,有GPU用GPU没有GPU用CPU
device = "cuda" if torch.cuda.is_available() else 'cpu'
# 讲模型放入到训练设备中
model = model.to(device)
# 初始化参数
test_corrects = 0.0
test_num = 0
# 只进行前向传播计算,不计算梯度,从而节省内存,加快运行速度
with torch.no_grad():
for test_data_x, test_data_y in test_dataloader:
# 将特征放入到测试设备中
test_data_x = test_data_x.to(device)
# 将标签放入到测试设备中
test_data_y = test_data_y.to(device)
# 设置模型为评估模式
model.eval()
# 前向传播过程,输入为测试数据集,输出为对每个样本的预测值
output= model(test_data_x)
# 查找每一行中最大值对应的行标
pre_lab = torch.argmax(output, dim=1)
# 如果预测正确,则准确度test_corrects加1
test_corrects += torch.sum(pre_lab == test_data_y.data)
# 将所有的测试样本进行累加
test_num += test_data_x.size(0)
# 计算测试准确率
test_acc = test_corrects.double().item() / test_num
print("测试的准确率为:", test_acc)
if __name__ == "__main__":
# 加载模型
model = VGG16()
model.load_state_dict(torch.load('best_model.pth'))
# # 利用现有的模型进行模型的测试
test_dataloader = test_data_process()
test_model_process(model, test_dataloader)
# 设定测试所用到的设备,有GPU用GPU没有GPU用CPU
device = "cuda" if torch.cuda.is_available() else 'cpu'
model = model.to(device)
classes = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat', 'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
with torch.no_grad():
for b_x, b_y in test_dataloader:
b_x = b_x.to(device)
b_y = b_y.to(device)
# 设置模型为验证模型
model.eval()
output = model(b_x)
pre_lab = torch.argmax(output, dim=1)
result = pre_lab.item()
label = b_y.item()
print("预测值:", classes[result], "------", "真实值:", classes[label])model_train.py
import copy
import time
import torch
from torchvision.datasets import FashionMNIST
from torchvision import transforms
import torch.utils.data as Data
import numpy as np
import matplotlib.pyplot as plt
from model import VGG16
import torch.nn as nn
import pandas as pd
def train_val_data_process():
train_data = FashionMNIST(root='./data',
train=True,
transform=transforms.Compose([transforms.Resize(size=224), transforms.ToTensor()]),
download=True)
train_data, val_data = Data.random_split(train_data, [round(0.8*len(train_data)), round(0.2*len(train_data))])
train_dataloader = Data.DataLoader(dataset=train_data,
batch_size=28,
shuffle=True,
num_workers=2)
val_dataloader = Data.DataLoader(dataset=val_data,
batch_size=28,
shuffle=True,
num_workers=2)
return train_dataloader, val_dataloader
def train_model_process(model, train_dataloader, val_dataloader, num_epochs):
# 设定训练所用到的设备,有GPU用GPU没有GPU用CPU
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# 使用Adam优化器,学习率为0.001
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
# 损失函数为交叉熵函数
criterion = nn.CrossEntropyLoss()
# 将模型放入到训练设备中
model = model.to(device)
# 复制当前模型的参数
best_model_wts = copy.deepcopy(model.state_dict())
# 初始化参数
# 最高准确度
best_acc = 0.0
# 训练集损失列表
train_loss_all = []
# 验证集损失列表
val_loss_all = []
# 训练集准确度列表
train_acc_all = []
# 验证集准确度列表
val_acc_all = []
# 当前时间
since = time.time()
for epoch in range(num_epochs):
print("Epoch {}/{}".format(epoch, num_epochs-1))
print("-"*10)
# 初始化参数
# 训练集损失函数
train_loss = 0.0
# 训练集准确度
train_corrects = 0
# 验证集损失函数
val_loss = 0.0
# 验证集准确度
val_corrects = 0
# 训练集样本数量
train_num = 0
# 验证集样本数量
val_num = 0
# 对每一个mini-batch训练和计算
for step, (b_x, b_y) in enumerate(train_dataloader):
# 将特征放入到训练设备中
b_x = b_x.to(device)
# 将标签放入到训练设备中
b_y = b_y.to(device)
# 设置模型为训练模式
model.train()
# 前向传播过程,输入为一个batch,输出为一个batch中对应的预测
output = model(b_x)
# 查找每一行中最大值对应的行标
pre_lab = torch.argmax(output, dim=1)
# 计算每一个batch的损失函数
loss = criterion(output, b_y)
# 将梯度初始化为0
optimizer.zero_grad()
# 反向传播计算
loss.backward()
# 根据网络反向传播的梯度信息来更新网络的参数,以起到降低loss函数计算值的作用
optimizer.step()
# 对损失函数进行累加
train_loss += loss.item() * b_x.size(0)
# 如果预测正确,则准确度train_corrects加1
train_corrects += torch.sum(pre_lab == b_y.data)
# 当前用于训练的样本数量
train_num += b_x.size(0)
for step, (b_x, b_y) in enumerate(val_dataloader):
# 将特征放入到验证设备中
b_x = b_x.to(device)
# 将标签放入到验证设备中
b_y = b_y.to(device)
# 设置模型为评估模式
model.eval()
# 前向传播过程,输入为一个batch,输出为一个batch中对应的预测
output = model(b_x)
# 查找每一行中最大值对应的行标
pre_lab = torch.argmax(output, dim=1)
# 计算每一个batch的损失函数
loss = criterion(output, b_y)
# 对损失函数进行累加
val_loss += loss.item() * b_x.size(0)
# 如果预测正确,则准确度train_corrects加1
val_corrects += torch.sum(pre_lab == b_y.data)
# 当前用于验证的样本数量
val_num += b_x.size(0)
# 计算并保存每一次迭代的loss值和准确率
# 计算并保存训练集的loss值
train_loss_all.append(train_loss / train_num)
# 计算并保存训练集的准确率
train_acc_all.append(train_corrects.double().item() / train_num)
# 计算并保存验证集的loss值
val_loss_all.append(val_loss / val_num)
# 计算并保存验证集的准确率
val_acc_all.append(val_corrects.double().item() / val_num)
print("{} train loss:{:.4f} train acc: {:.4f}".format(epoch, train_loss_all[-1], train_acc_all[-1]))
print("{} val loss:{:.4f} val acc: {:.4f}".format(epoch, val_loss_all[-1], val_acc_all[-1]))
if val_acc_all[-1] > best_acc:
# 保存当前最高准确度
best_acc = val_acc_all[-1]
# 保存当前最高准确度的模型参数
best_model_wts = copy.deepcopy(model.state_dict())
# 计算训练和验证的耗时
time_use = time.time() - since
print("训练和验证耗费的时间{:.0f}m{:.0f}s".format(time_use//60, time_use%60))
# 选择最优参数,保存最优参数的模型
model.load_state_dict(best_model_wts)
# torch.save(model.load_state_dict(best_model_wts), "C:/Users/86159/Desktop/LeNet/best_model.pth")
torch.save(best_model_wts, "C:/Users/86159/Desktop/VGG16/best_model.pth")
train_process = pd.DataFrame(data={"epoch":range(num_epochs),
"train_loss_all":train_loss_all,
"val_loss_all":val_loss_all,
"train_acc_all":train_acc_all,
"val_acc_all":val_acc_all,})
return train_process
def matplot_acc_loss(train_process):
# 显示每一次迭代后的训练集和验证集的损失函数和准确率
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot(train_process['epoch'], train_process.train_loss_all, "ro-", label="Train loss")
plt.plot(train_process['epoch'], train_process.val_loss_all, "bs-", label="Val loss")
plt.legend()
plt.xlabel("epoch")
plt.ylabel("Loss")
plt.subplot(1, 2, 2)
plt.plot(train_process['epoch'], train_process.train_acc_all, "ro-", label="Train acc")
plt.plot(train_process['epoch'], train_process.val_acc_all, "bs-", label="Val acc")
plt.xlabel("epoch")
plt.ylabel("acc")
plt.legend()
plt.show()
if __name__ == '__main__':
# 加载需要的模型
VGG16 = VGG16()
# 加载数据集
train_data, val_data = train_val_data_process()
# 利用现有的模型进行模型的训练
train_process = train_model_process(VGG16, train_data, val_data, num_epochs=20)
matplot_acc_loss(train_process)









Comments NOTHING