基本概念
1.基本术语
Attention
- 大写字母: 具有随机性的变量
- 小写字母: 实实在在的数值
- 代理(agent):需要控制的角色
- 环境(environment):角色所在的游戏
- 状态(state):角色所处的某一时刻的游戏场景
- 动作(action):能对角色能进行的操作
- 策略(policy):描述角色在某一状态产生某个动作的概率,控制角色在当前状态下所有动作的概率,不就是一种行动的决策。在环境
s,角色产生动作a的概率:π(a∣s)=P(A=a∣S=s) - 奖励(reward):在某一状态下,角色采取某一动作后,对该动作的评价
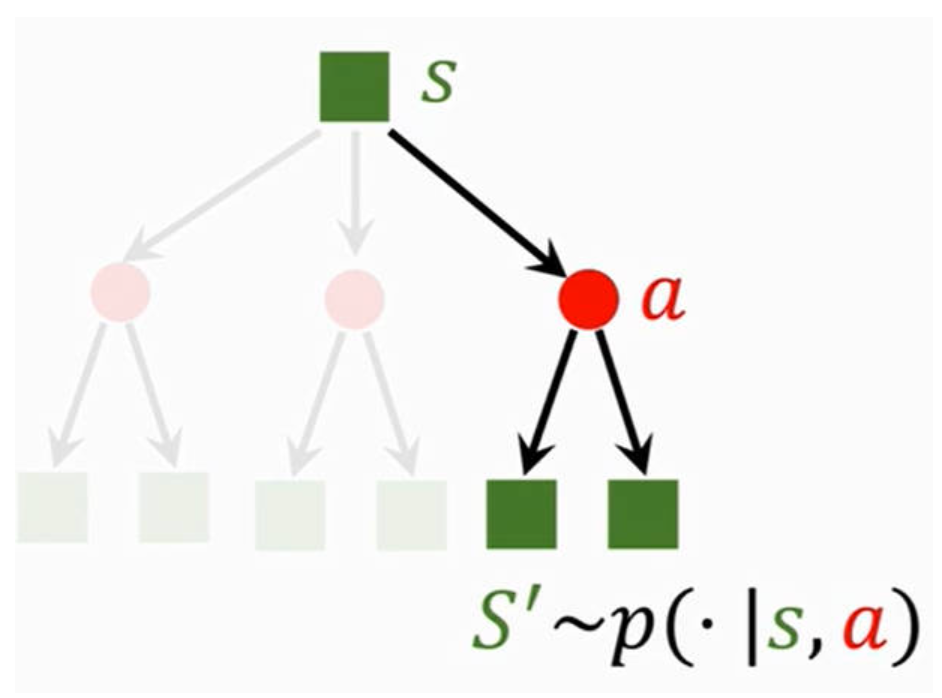
- 状态转移(state transition):从旧状态到新状态;状态转移是随机的,因为角色是不清楚游戏场景将如何变化。角色在旧环境
s,发生动作a后,游戏环境变为新状态s'的概率:p(s′∣s,a)=P(S′=s′∣S=s,A=a)
2.角色与环境的交互
2.1交互流程
- 角色根据「决策函数 π(a∣s) 」在当前环境状态下选择一个动作
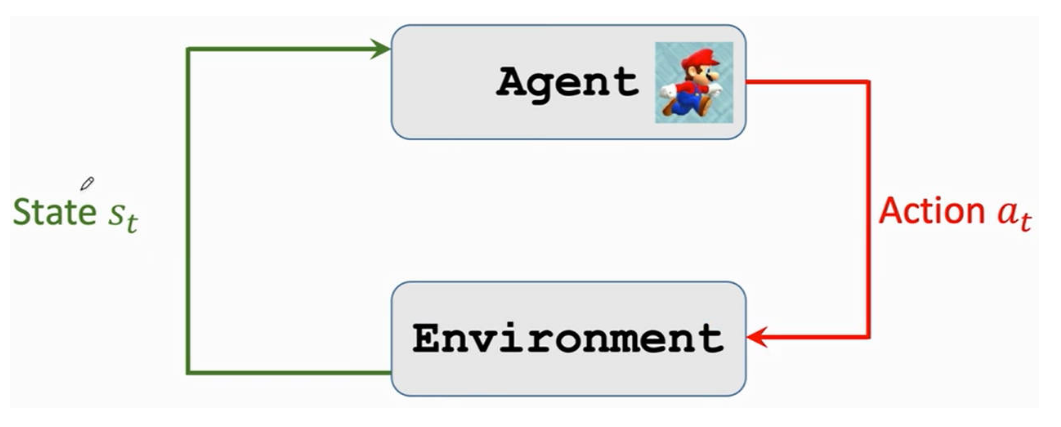
- 环境受到角色动作的影响进入下一个状态,并对角色的动作给出奖励。环境也根据「状态转移函数 p(s′∣s,z) 进入下一个状态
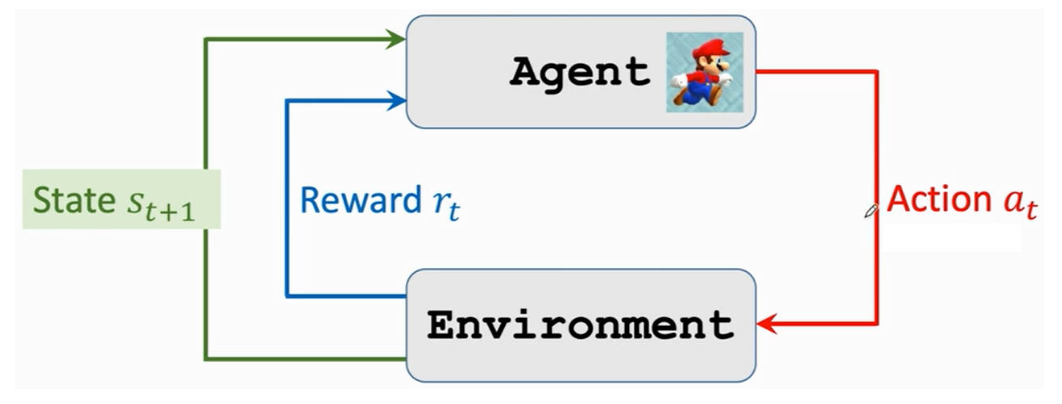
- 重复上述步骤
2.2随机性
- 动作的随机性:角色在当前状态下,会采取什么动作是随机的

- 状态转移的随机性:角色做出一个动作后,环境状态的变化是随机的
3.奖励,回报,价值函数
3.1奖励
奖励(reward): 对当前状态下的某一动作进行评价;「奖励」越大,说明离「目标」越接近,例如赢得本局游戏。
3.2回报
回报(return): 未来的累计奖励,即从当前时刻到结束的奖励之后。
折扣回报(discounted return): 由于当前奖励是马上能得到的,而未来的奖励变数较大,所以需要给未来的奖励降低比重。γγ 就为折扣率
Tip
回报(return)是具有「随机性」的。因为 UtUt 取决于 Rt+iRt+i ,而 Rt+iRt+i 又与将来的「状态」和「动作」有关。
3.3价值函数
- 动作价值函数(action-value function):由于「回报 Ut」是具有随机性的,并与将来的状态和动作有关,但是角色并不能知道未来会发生什么,所以角色在游戏过程中无法使用「回报」来评估当前的动作。为了对当前动作的价值进行评估,就对 UtUt 求解期望,过滤掉随机性。
其中,Qπ(st,at) 为动作价值函数,根据动作概率分布函数 π(at∣st) 进行计算,所以就不需要将来的 Rt+i 值参与计算。 st,at 均为小写字母,均是实实在在的数值,所以 Qπ(st,at) 是一个数值
- 最优动作价值函数(Optimal action-value function):由于「动作价值函数 Qπ 」与「策略函数 π」有关,不同的「策略函数」就会对应不同的「动作价值函数」。为了对「动作价值函数」进行统一,就选则使用「最优的策略函数」,因此「最优动作价值函数」主要用来评价「动作」的好坏
- 状态价值函数(state-value function): 对动作价值函数 Qπ(st,A) 关于自变量 A 进行期望计算。 由于 AA 是大写字母,是一个具有随机性的变量,Qπ(st,A) 则为一个关于 A 的函数 。Vπ(st) 可以用来评价角色当前所处状态的好坏
- 动作离散:
- 动作连续:
- 动作离散:
Tip
- 动作价值函数: 评价角色在状态
s所作出的动作a的好坏 - 状态价值函数: 评价角色在状态
s所处局势的好坏,例如当前不论做什么动作,都输定了
4.角色的控制
- 基于决策函数方案:给角色定制了一个非常棒的动作产生策略
- 观察游戏环境状态 st
- 根据决策函数 π(a∣st) 获取一个动作 at
- 基于最优动作价值函数方案:从所有可能的决策中,选择最优的动作
- 观察游戏环境状态 st
- 根据最优动作价值函数
- 学习的过程:不断的重复 (si,ai,ri)(si,ai,ri) 的过程,最终实现奖励的最大化。

价值学习
1.Deep Q-Network(DQN)
1.1算法思路
- 目标:赢得这场游戏,即实现「回报」最大。
- 策略:得到「最优价值函数 Q^∗(s,a) 」,这样就能通过带入状态 s,解算出最优动作
- 问题: Q^∗(s,a) 只能通过上帝视角得到,角色是无法认知。
- 解决:利用一个神经网络 Q(s,a;w) 来近似拟合出 Q^∗(s,a)
s:神经网络的输入a:神经网络的输出w:神经网络的参数
1.2DQN神经网络构造
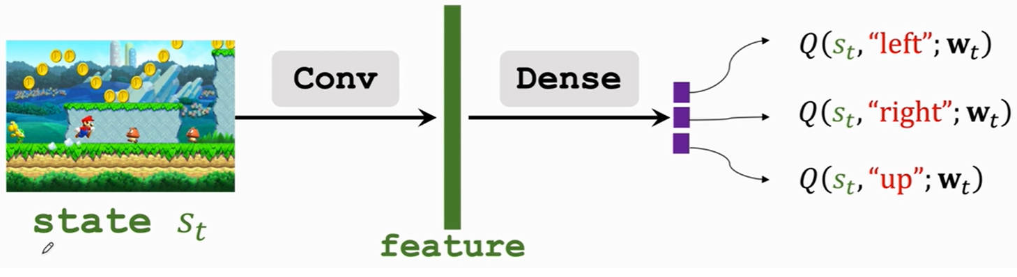
- 一张游戏画面当作一个「状态」,状态通过「卷积层」实现特征提取
- 特征输入给「权连接层」进行 Q^∗(s,a)拟合
- 「权连接层」输出每个动作的 Q^∗(s,a)结果
1.3DQN运行流程
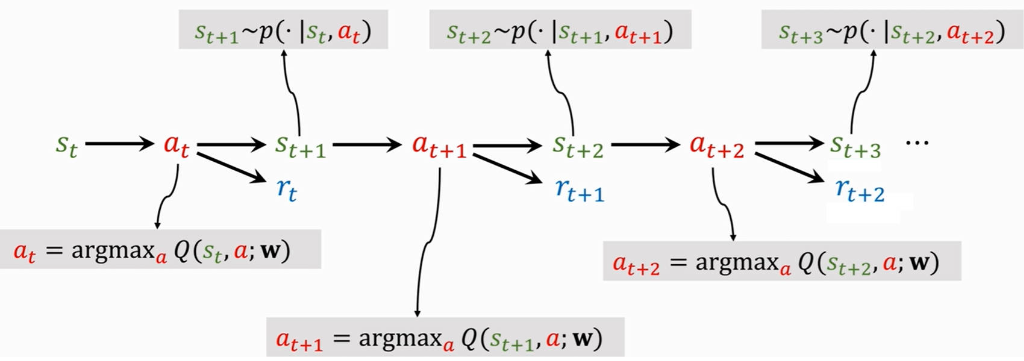
- 通过当前的状态 stst,利用神经网络计算出当前最优的动作
- 执行动作
后,给出奖励
- 环境状态转移,得到下一个状态
- 重复上述步骤
2.DQN训练
2.1时间差分算法(Tenporal Different)
1. 问题模型

问题: 设计一个神经网络 Q(w)Q(w),对从NYC驾驶到atlanta所要花费的时间进行预测。
2. 梯度下降算法
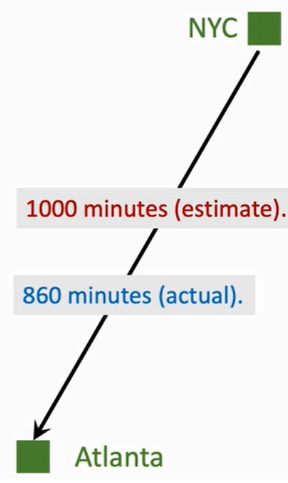
- 模型估计时间: q=Q(w)=1000min
- 真实驾驶时间: y=860min
- 计算损失值:L=12(q−y)2
- 计算关于系数 w 的梯度:∂L∂w=∂L∂q∂q∂w=(q−y)∂Q(w)∂w∂w∂L=∂q∂L∂w∂q=(q−y)∂w∂Q(w)
- 更新系数:w=w−α∂L∂w
Tip
梯度下降法只能利用从NYC驾驶到atlanta跑完全程的时间作为真实时间 yy 进行计算,不能利用其中一段的时间。而DT算法则对这个情况进行改进。
3. 时间差分算法
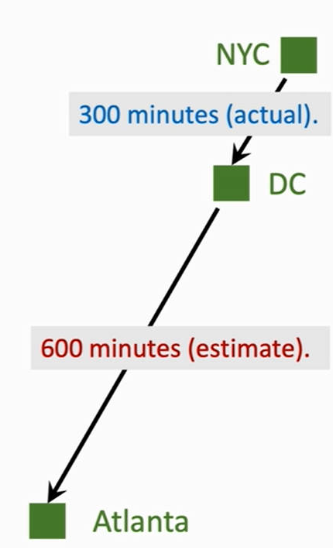
- 模型估计时间: q=Q(w)=1000min;
- 真实驾驶时间只有从
NYC到DC的 300 min,剩余的路程可以通过模型估计:y=300+600=900miny=300+600=900min - 计算损失值:L=12(q−y)2L=21(q−y)2
- 计算关于系数 ww 的梯度:∂L∂w=∂L∂q∂q∂w=(q−y)∂Q(w)∂w∂w∂L=∂q∂L∂w∂q=(q−y)∂w∂Q(w)
- 更新系数:w=w−α∂L∂ww=w−α∂w∂L
Tip
- TD目标:TD算法中的
y - TD误差:D算法中的
q - y
2.2 TD训练DQN
思路: 由于DQN算法的目标是实现 UtUt 的最大化
Ut=Rt+γRt+1+γ2Rt+2+γ3Rt+3+⋯Ut+1=Rt+1+γRt+2+γ2Rt+3+⋯UtUt+1=Rt+γRt+1+γ2Rt+2+γ3Rt+3+⋯=Rt+1+γRt+2+γ2Rt+3+⋯
对公式进行简化
Ut=Rt+γUt+1Ut=Rt+γUt+1
将上述公式与DT算法进行对照:
- UtUt 与 Ut+1Ut+1 就是 Q(s,a;w)Q(s,a;w) 模型的预测值:Q(st,at;w)Q(st,at;w) 、Q(st+1,at+1;w)Q(st+1,at+1;w)
- RtRt就是一次工况下的部分真实测量值
- TD目标就为:yt=Rt+γQ(st+1,at+1;w)=Rt+γ max Q(st+1,a;w)yt==Rt+γQ(st+1,at+1;w)Rt+γ max Q(st+1,a;w)
- TD误差就为:Q(st,at;w)−[Rt+γQ(st+1,at+1;w)]Q(st,at;w)−[Rt+γQ(st+1,at+1;w)]
策略学习
1.算法思路
- 目标:控制动作执行的概率,使得最终的「状态激活函数」的结果最大,即动作执行后,使得平均局势最优( ES[Vπ(s)]ES[Vπ(s)] 值最大 )。
- 策略:得到「策略函数 π(a∣s)π(a∣s)」,这样就能通过带入状态 ss,根据动作的发生的概率随机选择动作。
- 问题:要使得局势最优,就要知道每种状态下最优的 π(a∣s)π(a∣s) ,但是角色无法认知。
- 解决:利用一个神经网络 π(a∣s;θ)π(a∣s;θ) 来近似拟合出 每种状态下应当采取的 π(a∣s)π(a∣s)
s:神经网络的输入a:神经网络的输出- θθ:神经网络的参数
2.神经网络的构造
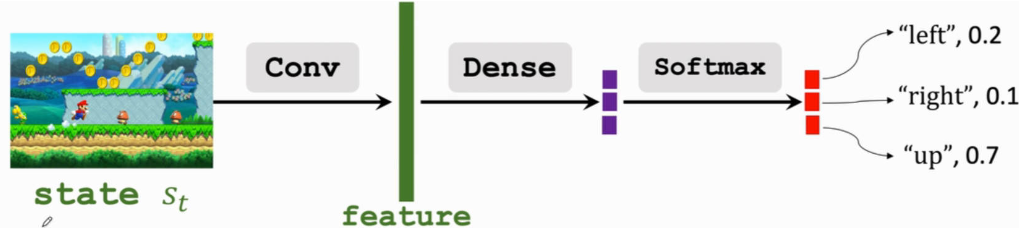
- 一张游戏画面当作一个「状态」,状态通过「卷积层」实现特征提取
- 特征输入给「权连接层」进行 π(a∣s)π(a∣s) 拟合
- 将「权连接层」的输出通过
softmax层转化为概率 - 输出每个动作在当前状态下产生好结果的概率
3.策略梯度训练
- 目标函数: V(st;θ)=EA[Qπ(st,A)]=∑aπ(a∣st;θ)Qπ(st,a)J(θ)=ES[V(S;θ)]V(st;θ)J(θ)=EA[Qπ(st,A)]=a∑π(a∣st;θ)Qπ(st,a)=ES[V(S;θ)]
- 参数更新: 由于 ES[V(S;θ)]ES[V(S;θ)] 不好计算,所以使用 V(S;θ)V(S;θ) 来近似;由于求解的是 J(θ)J(θ) 最大,所以使用的是
+θ=θ+β∂V(s;θ)∂θθ=θ+β∂θ∂V(s;θ)
4.策略梯度算法
定义: ∂V(s;θ)∂θ∂θ∂V(s;θ) 就是策略梯度。
计算: 将策函数关于θθ求导展开
∂V(s;θ)∂θ=∂∑aπ(a∣s;θ)Qπ(s,a)∂θ=∑a(∂π(a∣s;θ)∂θQπ(s,a)+∂Qπ(s,a)∂θπ(a∣s;θ))∂θ∂V(s;θ)=∂θ∂a∑π(a∣s;θ)Qπ(s,a)=a∑(∂θ∂π(a∣s;θ)Qπ(s,a)+∂θ∂Qπ(s,a)π(a∣s;θ))
由于 Qπ(s,a)Qπ(s,a) 求解关于 θθ 的导数也困难,所以忽略掉
∂V(s;θ)∂θ=∑a∂π(a∣s;θ)∂θQπ(s,a)∂θ∂V(s;θ)=a∑∂θ∂π(a∣s;θ)Qπ(s,a)
对于上述公式只能求解离散形式,连续形式可以变形为:
∂V(s;θ)∂θ=∫aπ(a∣s;θ)∂lnπ(a∣s;θ)∂θQπ(s,a) da=EA[∂lnπ(a∣s;θ)∂θQπ(s,a)]∂θ∂V(s;θ)=∫aπ(a∣s;θ)∂θ∂lnπ(a∣s;θ)Qπ(s,a) da=EA[∂θ∂lnπ(a∣s;θ)Qπ(s,a)]
可以利用 蒙特卡洛积分 对上述期望进行近似计算。
- 根据策略函数 π(a∣s;θ)π(a∣s;θ) 随机获取动作 a^a^
- 带入 a^a^ 计算:g(a^,θ)=∂lnπ(a^∣s;θ)∂θQπ(s,a^)g(a^,θ)=∂θ∂lnπ(a^∣s;θ)Qπ(s,a^)
- 然后通过 g(a^,θ)g(a^,θ) 来近似计算:∂V(s;θ)∂θ=EA[g(A,θ)]∂θ∂V(s;θ)=EA[g(A,θ)]
5.价值函数计算
- 方法一: 角色游玩一局游戏后,再计算一次 Qπ(st,at)Qπ(st,at) ,然后用该值来近似代替,这样就导致一局游戏才能更新一次θθ系数。
- 方法二: 对 Qπ(st,at)Qπ(st,at) 再建立一个神经网络
TD算法
1.sarsa
1.1 TD目标
- 折扣回报: Ut=Rt+γUt+1Ut=Rt+γUt+1
- 动作价值:Qπ(st,at)=E[Ut∣st,at]=E[Rt+γUt+1∣st,at]=E[Rt]+γE[Ut+1∣st,at]=E[Rt]+γE[Qπ(St+1,At+1)∣st,at]=E[Rt+γQπ(St+1,At+1)]Qπ(st,at)=E[Ut∣st,at]=E[Rt+γUt+1∣st,at]=E[Rt]+γE[Ut+1∣st,at]=E[Rt]+γE[Qπ(St+1,At+1)∣st,at]=E[Rt+γQπ(St+1,At+1)]
- TD目标: 对「动作价值」进行蒙特卡洛近似,得 yt=rt+γQπ(st+1,at+1)yt=rt+γQπ(st+1,at+1)
1.2.表格形式
形式:利用一个表格来记录 Qπ(s,a)Qπ(s,a),行为状态 ss,列为动作 aa。
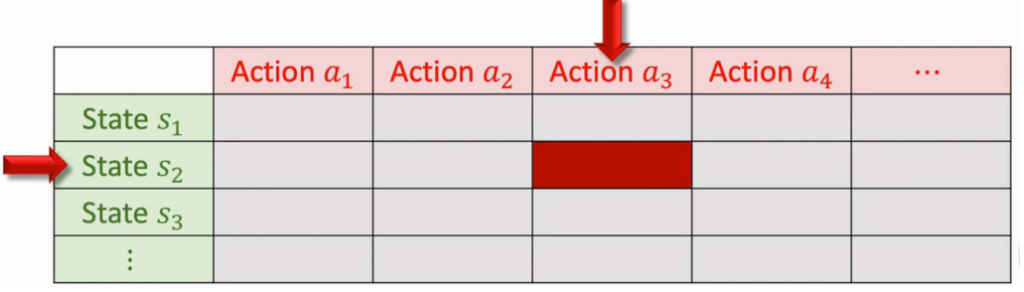
算法:
- 观测一次状态:(st,at,rt,st+1)(st,at,rt,st+1)
- 根据状态 st+1st+1,通过策略函数 π(a∣s)π(a∣s) 预测下一个动作 at+1at+1
- TD目标:yt=rt+γQπ(st+1,at+1)yt=rt+γQπ(st+1,at+1)
- TD误差:δt=Qπ(st,at)−ytδt=Qπ(st,at)−yt
- 更新 QπQπ:Qπ(st,at)=Qπ(st,at)−αδtQπ(st,at)=Qπ(st,at)−αδt
- Sarsa案例
1.3 Sarsa(λ)
1.3.1 Sarsa表格的问题
- 问题:
- Sarsa 算法对于 QπQπ 更新,为单步更新,角色动一次便更新一次 QπQπ,这就导致一回合游戏结束后,回顾寻宝「轨迹」,发现在宝藏附近的状态的 QπQπ 才与宝藏关系密切,而前往宝藏之前的轨迹状态则认为与宝藏无关。这就会导致 Sarsa 要在同样的轨迹上重复多次,进行 QπQπ 的更新,才能得到较好的 QπQπ,前提是找到宝藏的情况下,前期没有找到时,决策的随机数得大一些
- 角色可能在前进的轨迹上转圈(在某几个状态上来回切换)
-
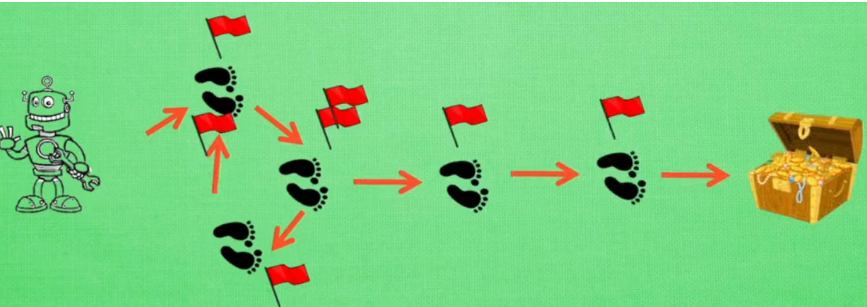
- 解决思路:
- 利用多组状态对 QπQπ 进行更新,增强轨迹上各个状态与宝藏的关联性
- 对轨迹上的每个状态进行「标记」,标记值越大的状态,说明该状态对找到宝藏的贡献越大,尽量避免没必要的转圈
1.3.2 Sarsa(λ)的实现
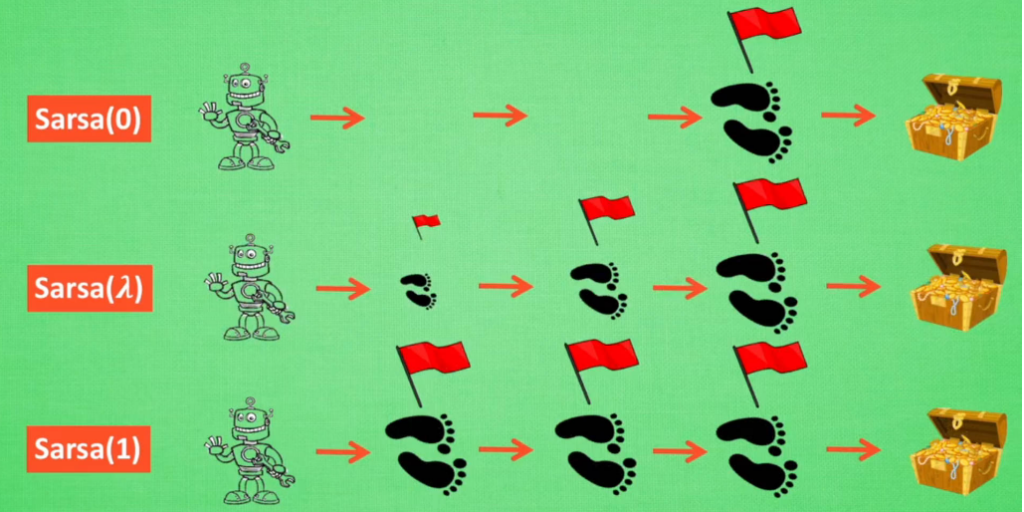
- 状态个数: 利用多少个状态对 QπQπ 进行更新,这里的取值范围为
1 ~ n(n:表示一回合结束时,轨迹所包含状态的个数),但是由于我们不会真的一回合才进行更新,所以并不知道一回合会有多少状态。因此,可以将状态个数映射到 [0,1],0:表示1个状态;1:表示n个状态,而我们用于Sarsa更新,使用的状态个数为 λ∈[0,1]λ∈[0,1],所以该算法就称之为 Sarsa(λλ) - 状态标记:
- 一回合中,每个被经过的状态的标记值都会被记录,放到一个
eligibility_trace表中 - 每个状态被经过一次,将会被标记,标记会随时间衰减

- 当一个状态被多次经过时,对于标记值的处理方式有两种
- 标记值直接叠加
- 标记值限幅
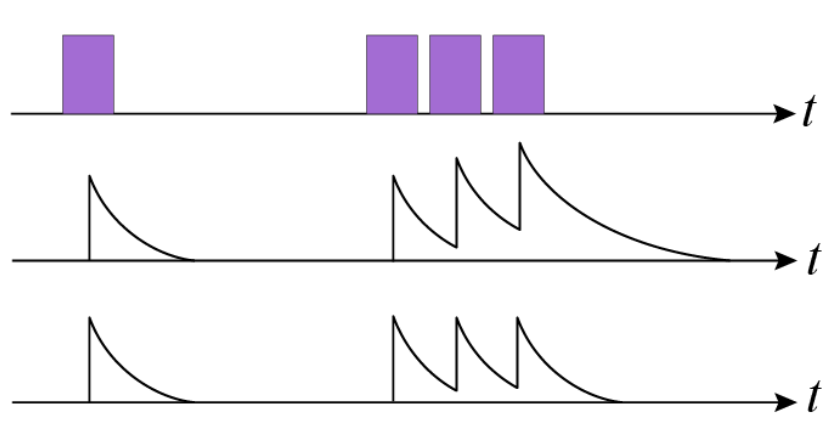
- 一回合中,每个被经过的状态的标记值都会被记录,放到一个
- 算法流程:每一轮游戏的开始前,都会将轨迹表归零,E=0E=0
- 观测一次状态:(st,at,rt,st+1)(st,at,rt,st+1)
- 根据状态 st+1st+1,通过策略函数 π(a∣s)π(a∣s) 预测下一个动作 at+1at+1
- TD目标:yt=rt+γQπ(st+1,at+1)yt=rt+γQπ(st+1,at+1)
- TD误差:δt=Qπ(st,at)−ytδt=Qπ(st,at)−yt
- 更新的轨迹表EE:
- 方式一:E(st,at)=E(st,at)+1E(st,at)=E(st,at)+1
- 方式二:E(st,:)=0; E(st,at)=1E(st,:)=0; E(st,at)=1
- 更新 QπQπ 全表:Qπ=Qπ−αδtEQπ=Qπ−αδtE
- 实现 EE 全表中标记值的衰减:E=γλEE=γλE
- Sarsa(λ)案例
1.3.3 Sarsa(λ)的解释
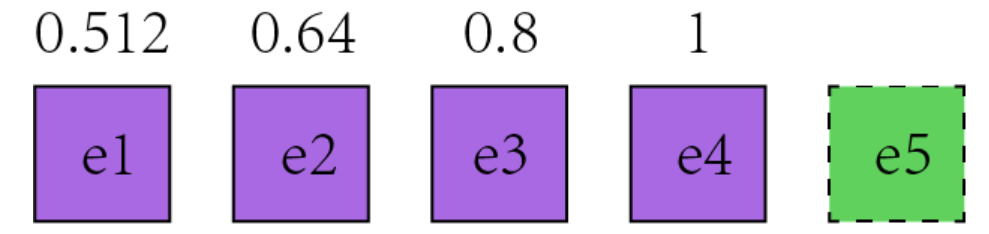
e4时刻的QπQπ 更新: 在e4时刻,对于 Q(e4)Q(e4) 的TD误差为 δq4=Q(e4)−r4−γQ(e5)δq4=Q(e4)−r4−γQ(e5) 并对 Q(e4)Q(e4) 进行修正 Q(e4)′=Q(e4)−αδq4Q(e4)′=Q(e4)−αδq4 在e3时刻,对于 Q(e3)Q(e3) 的TD误差为 δq3=Q(e3)−r3−γQ(e4)δq3=Q(e3)−r3−γQ(e4) 在e3时,我们并不知道Q(e4)具有误差的情况下,对Q(e3)Q(e3)进行了修正 Q(e3)′=Q(e3)−αδq3Q(e3)′=Q(e3)−αδq3 在e4时刻,我们得到了更准确的 Q(e4)′Q(e4)′ ,回代修正 Q(e3)Q(e3) δq3′=Q(e3)−r3−γQ(e4)′=Q(e3)−r3−γ[Q(e4)−αδq4]=Q(e3)−r3−γQ(e4)+γαδq4=δq3+γδq4δq3′=Q(e3)−r3−γQ(e4)′=Q(e3)−r3−γ[Q(e4)−αδq4]=Q(e3)−r3−γQ(e4)+γαδq4=δq3+γδq4 重新对Q(e3)Q(e3)进行修正 Q(e3)′′=Q(e3)−αδq3′=Q(e3)−αδq3−αγδq4=Q(e3)′−αδq4γQ(e3)′′=Q(e3)−αδq3′=Q(e3)−αδq3−αγδq4=Q(e3)′−αδq4γ 最终得到的公式就与计算流程的更新公式所对应: Q(e3)′′=Q(e3)′−αδq4γQπ=Qπ−αδtEQ(e3)′′Qπ=Q(e3)′−αδq4γ=Qπ−αδtE 其他状态同理,就是一层一层的套娃下去。- QπQπ 更新: 对于上述的 Sarsa(λλ) 算法,并非是一轮游戏结束后,才对 QπQπ 表进更新。从算法的计算流程可以看出 QπQπ 表在每一次动作后,都会更新一次,也就是说,角色每转移一次状态,就会停下来,对之前的轨迹进行一次回顾,修正之前所经历的状态到当前状态 stst 的关联性。
- 状态个数: 在
e4时刻,对于轨迹状态e1的动作价值 QπQπ 更新,涉及的状态就有e2 - e4;对于轨迹状态e2而言,就是e3 - e4 - λλ 实现状态个数控制:
- λ=0λ=0:这就导致一下次状态的开始,E=0E=0,然后轨迹表只有当前状态才有记录:E(st,at)=1E(st,at)=1,因此 Qπ=Qπ−αδtEQπ=Qπ−αδtE 实际只更新了当前状态的 Qπ(st,at)Qπ(st,at)。
- λ=1λ=1:Qπ=Qπ−αδtEQπ=Qπ−αδtE 更新了 从回合开始状态 s0s0 到当前状态 stst 对应的所有 QπQπ值
- λ∈(0,1)λ∈(0,1):由于 E=γλEE=γλE 的反复迭代,实现了轨迹标记值的衰减,离当前状态越近的状态,其标记值越大,例如到达
e4时刻时,e4 = 1;e3 = 0.8;e2 = 0.64,时间越靠前,e值就越小,对e值再乘以一个倍数值 λλ,就可以将原来当前时刻的e值变得更小,几乎就等于0了,这样就实现了类似于 λ=0λ=0 时,状态的 QπQπ 不更新。即 λλ 使得比较旧的 QpiQpi 不再参与到更新,也就控制了「状态个数」
1.4神经网络价值
思路: 利用神经网络 q(s,a;w)q(s,a;w) 来近似动作价值函数 Qπ(s,a)Qπ(s,a)。 输入为状态,输出为各个动作对应的价值
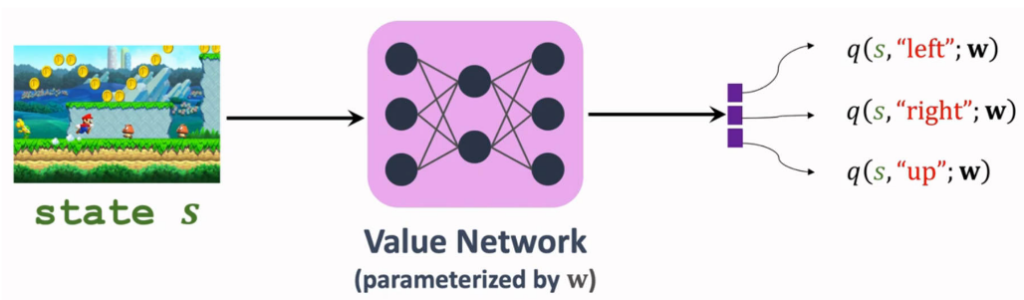
算法:
- 观测一次状态:(st,at,rt,st+1)(st,at,rt,st+1)
- 根据状态 st+1st+1,通过策略函数 π(a∣s)π(a∣s) 预测下一个动作 at+1at+1
- TD目标:yt=rt+γq(st+1,at+1;w)yt=rt+γq(st+1,at+1;w)
- TD误差:δt=q(st,at;w)−ytδt=q(st,at;w)−yt
- 损失函数:L=12δt2L=21δt2
- 更新系数:w=w−αδt∂q(st,at;w)∂ww=w−αδt∂w∂q(st,at;w)
2.Q Learning
2.1 TD目标
- 最优动作价值:Qπ(st,at)=E[Rt+γQπ(St+1,At+1)]Q∗(st,at)=E[Rt+γQ∗(St+1,At+1)]=E[Rt+γmaxaQ∗(St+1,a)]Qπ(st,at)Q∗(st,at)=E[Rt+γQπ(St+1,At+1)]=E[Rt+γQ∗(St+1,At+1)]=E[Rt+γamaxQ∗(St+1,a)]
- TD目标: 对「最优动作价值」进行蒙特卡洛近似,得 yt=rt+γmaxaQ∗(st+1,a)yt=rt+γamaxQ∗(st+1,a)
2.2表格形式
形式:利用一个表格来记录 Q∗(s,a)Q∗(s,a),行为状态 ss,列为动作 aa。
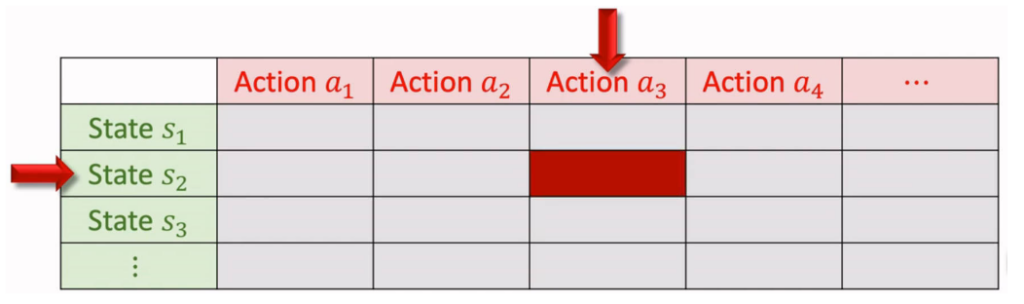
- 观测一次状态:(st,at,rt,st+1)(st,at,rt,st+1)
- TD目标:yt=rt+γmaxaQ∗(st+1,a)yt=rt+γamaxQ∗(st+1,a)
- TD误差:δt=Q∗(st,at)−ytδt=Q∗(st,at)−yt
- 更新 QπQπ:Q∗(st,at)=Q∗(st,at)−αδtQ∗(st,at)=Q∗(st,at)−αδt
- Q learning 案例
2.3神经网络形式
思路: 利用神经网络 Q(s,a;w)Q(s,a;w) 来近似动作价值函数 Q∗(s,a)Q∗(s,a)。
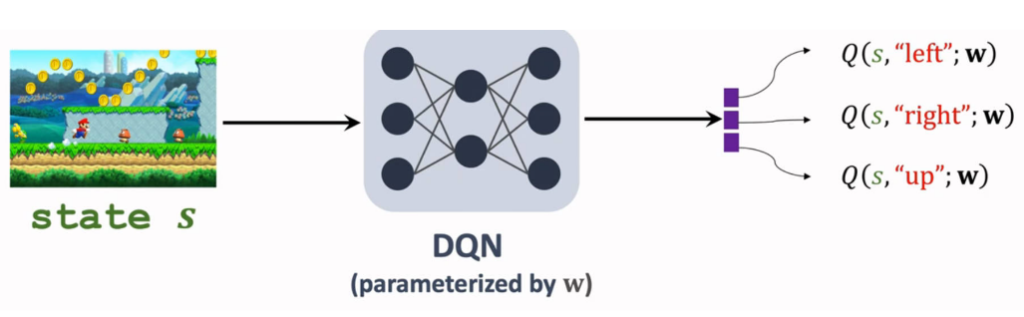
算法:
- 观测一次状态:(st,at,rt,st+1)(st,at,rt,st+1)
- TD目标:yt=rt+γmaxaQ(st+1,a;w)yt=rt+γamaxQ(st+1,a;w)
- TD误差:δt=Q(st,at;w)−ytδt=Q(st,at;w)−yt
- 损失函数:L=12δt2L=21δt2
- 更新系数:w=w−αδt∂q(st,at;w)∂ww=w−αδt∂w∂q(st,at;w)
Note
- sarsa: 近似的是「价值函数 Qπ(s,a)Qπ(s,a)」
- Q Learning: 近似的是「最优价值函数 Q∗(s,a)Q∗(s,a)」
- 神经网络版的 Q Learning 就是 DQN 算法
3.multi-step TD
- 思路: 之前的算法都是利用一次 rr 进行算法更新,还可以采用多次 rr 来更新算法。
- multi-step TD 目标: 利用多次 rr 构造的TD目标
- 回报展开: Ut=Rt+γUt+1=Rt+γRt+1+γ2Ut+2=Rt+γRt+1+γ2Rt+2+γ3Ut+3=∑i=0m−1γiRt+i+γmUt+mUt=Rt+γUt+1=Rt+γRt+1+γ2Ut+2=Rt+γRt+1+γ2Rt+2+γ3Ut+3=i=0∑m−1γiRt+i+γmUt+m
- sarsa multi-step TD 目标: yt=∑i=0m−1γirt+i+γmQπ(st+m,at+m)yt=i=0∑m−1γirt+i+γmQπ(st+m,at+m)
- sarsa multi-step TD 目标: yt=∑i=0m−1γirt+i+γmmaxaQ∗(st+m,a)yt=i=0∑m−1γirt+i+γmamaxQ∗(st+m,a)
Actor-Critic算法
1.算法概念
思路: 在 策略学习 对 Qπ(st,at)Qπ(st,at) 的计算是用一次回合后得到的 UU 进行近似。同样对于 Qπ(st,at)Qπ(st,at) 也可以再建立一个神经网络进行拟合。
策略网络 π(a∣s;θ)π(a∣s;θ) : 用于对策略函数的近似,即Actor,控制角色的动作
价值网络 q(s,a;w)q(s,a;w) : 用于对价值函数的近似,即Critic,对角色动作进行打分
总目标: 使得最终的状态价值函数的值最大,V(s;θ,w)=∑aπ(a∣s;θ)q(s,a;w)V(s;θ,w)=a∑π(a∣s;θ)q(s,a;w)
2.网格模型
策略网络:
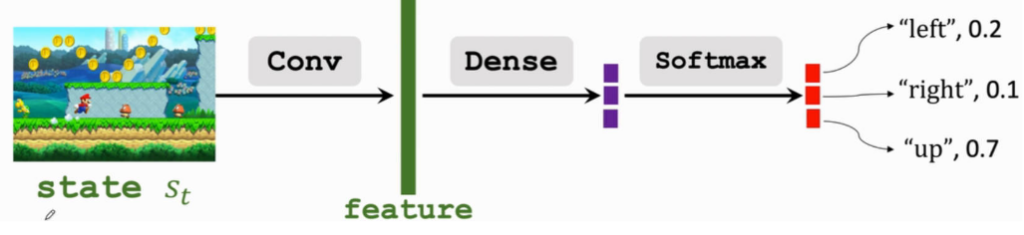
- 一张游戏画面当作一个「状态」,状态通过「卷积层」实现特征提取
- 特征输入给「权连接层」进行 π(a∣s)π(a∣s) 拟合
- 将「权连接层」的输出通过
softmax层转化为概率 - 输出每个动作在当前状态下产生好结果的概率
价值网络

- 一张游戏画面当作一个「状态」,状态通过「卷积层」实现特征提取
- 要评价的一个「动作」通过权连接层进行特征提取
- 将「状态」与「动作」特征进行组合,最后输入一个权连接层,得到「评分」
3.网格训练
目标:
- 策略网络: 价值函数 V(s)V(s) 的值最大化
- 价值网络: 对动作的打分 q(s,a)q(s,a) 更接近真实值
参数更新:
- 观测到环境状态 stst
- 根据 π(a∣s;θ)π(a∣s;θ) 得到动作 atat
- 角色执行动作 atat,然后获取状态 st+1st+1 与奖励 rtrt
- 根据TD算法更新系数 ww
- 根据策略梯度算法更新系数 θθ
系数 ww 更新:
- 计算 q(st,at;wt)q(st,at;wt)
- 根据状态 st+1st+1,通过 π(a∣s;θ)π(a∣s;θ) 预测动作 atat ,然后计算 q(st+1,at+1;wt)q(st+1,at+1;wt)
- 计算TD目标:yt=rt+γq(st+1,at+1;wt)yt=rt+γq(st+1,at+1;wt)
- 损失函数:L(w)=12[q(st,at;wt)−yt]2L(w)=21[q(st,at;wt)−yt]2
- 更新参数:wt+1=wt−α∂L(w)∂wwt+1=wt−α∂w∂L(w)
系数 θθ 更新:
- 根据策略函数 π(a∣st;θt)π(a∣st;θt) 随机获取动作 a^a^
- 带入 a^a^ 计算:g(a^,θt)=∂lnπ(a^∣s;θt)∂θq(st,a^;w)g(a^,θt)=∂θ∂lnπ(a^∣s;θt)q(st,a^;w)
- 然后通过 g(a^,θt)g(a^,θt) 来近似计算:∂V(s;θt)∂θt=EA[g(A,θt)]∂θt∂V(s;θt)=EA[g(A,θt)]
- 更新参数:θt+1=θt+βg(a,θt)θt+1=θt+βg(a,θt)
Note
再计算 g(a,θ)g(a,θ) 时,一般会使用TD error:
δt=q(st,at;wt)−[rt+γq(st+1,at+1;wt)]δt=q(st,at;wt)−[rt+γq(st+1,at+1;wt)]
来代替 q(st,a;w)q(st,a;w),这样可以使算法收敛加快。
DQN优化
1.经验回放
1.1概念
传统DQN的缺陷:
- 传统的DQN,一次 (st,at,rt,st+1)(st,at,rt,st+1) 只用于一次计算,十分浪费
- 用于训练的 (st,at,rt,st+1)(st,at,rt,st+1) 具有较强的相关性(stst训练完,就使用 st+1st+1),这种相关性是有害的
经验回放(experience replay):
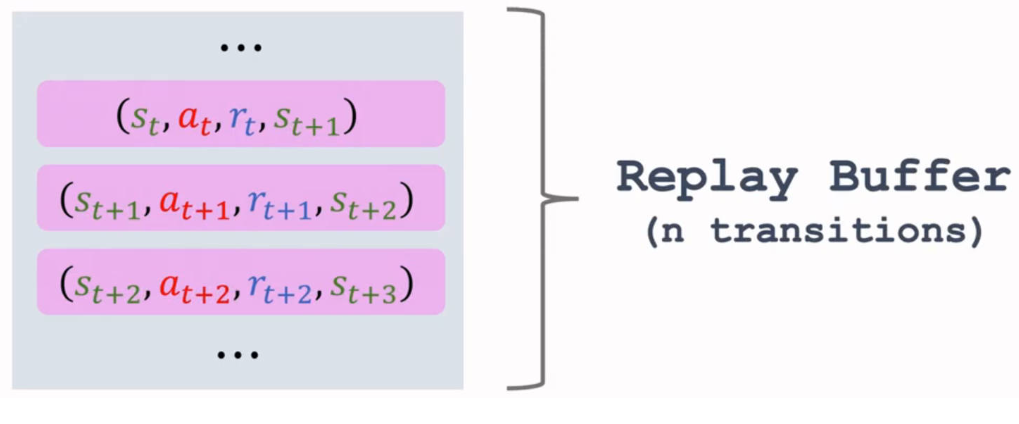
- 将每一次 (st,at,rt,st+1)(st,at,rt,st+1) 都放入一个「回放缓冲区
replay buffer」中。缓冲区大小一定,存满后,就进行入队和出队 - 利用「随机梯度
SGD」进行模型的更新: 从回放缓冲区中,随机抽取一项进行模型更新计算
1.2优先经验回放
原因: 角色对于常规的游戏环境会在「回放缓冲区」中存放大量的经验,而对于BOSS关卡的经验却很少。对于经验回放,若采用均匀抽样,就会导致对BOSS关卡的学习机会变少。

优先经验回放: 对于特殊状态(例如BOSS关卡),增加其被抽中学习的概率。
- 实现方法: ∣δt∣∣δt∣ 越大,被抽中的概率越大
- 方法一: pt∝∣δt∣+ϵpt∝∣δt∣+ϵ,即被抽样的概率 ptpt 正比于TD error绝对值 ∣δt∣∣δt∣
- 方法二: pt∝1ipt∝i1,其中
i是状态根据 ∣δt∣∣δt∣ 降序排列的索引。
- 学习率: (npt)−βα,β∈(0,1)(npt)−βα,β∈(0,1),即被抽中的概率越大,学习率应当越小。 用于消除大概率抽样,造成的预测偏差
- 更新 ∣δt∣∣δt∣:
- 初始值设置为最大值。因为状态只有进行一次学习计算后才能知道结果
- 每一次学习后,更新对于状态的 ∣δt∣∣δt∣

2.高估问题
2.1 高估的问题
1. 最大化
定理: x1,x2,⋯ ,xnx1,x2,⋯,xn是真实序列;Q1,Q2,⋯ ,QnQ1,Q2,⋯,Qn是真实值带有均值为 00 噪声的观测值。就存在
E[mean(Qi)]=mean(xi)E[max(Qi)]≥max(xi)E[min(Qi)]≤min(xi)E[mean(Qi)]E[max(Qi)]E[min(Qi)]=mean(xi)≥max(xi)≤min(xi)
预测值高估: TD目标为 yt=rt+γmaxaQ(st+1,a;w)yt=rt+γamaxQ(st+1,a;w) ,根据上述定理可知,maxaQ(st+1,a;w)amaxQ(st+1,a;w) 的值相对于真实值,其实被放大了,进一步导致 ytyt 的值被高估。由于 ytyt 是目标,这就使得DQN模型的预测值被高估。
2. 自举
在TD目标中 yt=rt+γmaxaQ(st+1,a;w)yt=rt+γamaxQ(st+1,a;w),Q(st+1,a;w)Q(st+1,a;w) 其实已经被模型高估计算了,这个高估的值又被回代用来更新 Q(st,a;w)Q(st,a;w) 的值,这就使得高估值被迭代放大。
2.2高估的危害
由于DQN对于 Q(s,a;w)Q(s,a;w) 的高估并非均匀的,这就导致最后的预测结果大小关系的改变。这就导致「动作」的选择,可能是错误的。
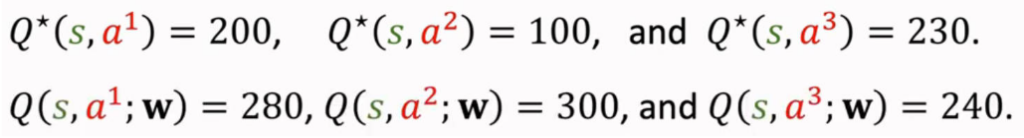
2.3目标网络
算法:
- 观测一次状态:(st,at,rt,st+1)(st,at,rt,st+1)
- TD目标:yt=rt+γmaxaQ(st+1,a;w−)yt=rt+γamaxQ(st+1,a;w−)
- TD误差:δt=Q(st,at;w)−ytδt=Q(st,at;w)−yt
- 损失函数:L=12δt2L=21δt2
- 更新 Q(st,at;w)Q(st,at;w) 系数:w=w−αδt∂Q(s,a;w)∂ww=w−αδt∂w∂Q(s,a;w)
- 更新 Q(s,a;w−)Q(s,a;w−) 系数: 要一段时间才更新一次
- 方法一: w−=ww−=w
- 方法二: w−=τw+(1−τ)w−w−=τw+(1−τ)w−
Note
「目标网络targe network」方法是利用「目标网络(Q(st+1,a;w−)Q(st+1,a;w−))」来代替「TD目标」中预测下一动作的动作价值的网络 Q(st+1,a;w)Q(st+1,a;w)。该方法避免自举。
2.4 Double DQN
算法:
- 观测一次状态:(st,at,rt,st+1)(st,at,rt,st+1)
- 选择下一动作:a∗=maxaQ(st+1,a;w)a∗=amaxQ(st+1,a;w)
- TD目标:yt=rt+γQ(st+1,a∗;w−)yt=rt+γQ(st+1,a∗;w−)
- TD误差:δt=Q(st,at;w)−ytδt=Q(st,at;w)−yt
- 损失函数:L=12δt2L=21δt2
- 更新 Q(st,at;w)Q(st,at;w) 系数:w=w−αδt∂Q(s,a;w)∂ww=w−αδt∂w∂Q(s,a;w)
- 更新 Q(s,a;w−)Q(s,a;w−) 系数: 要一段时间才更新一次
- 方法一: w−=ww−=w
- 方法二: w−=τw+(1−τ)w−w−=τw+(1−τ)w−
[note]
double DQN算法中,对于计算TD目标,利用 Q(st+1,a;w)Q(st+1,a;w)提供预测动作 a∗a∗,然后利用「目标网络」 Q(st+1,a∗;w−)Q(st+1,a∗;w−) 进行计算。
3. Dueling Network
3.1概念
最优动作价值: Q∗(s,a)=maxπQπ(s,a)Q∗(s,a)=πmaxQπ(s,a)
最优状态价值: V∗(s)=maxπVπ(s)V∗(s)=πmaxVπ(s)
优势函数(optimal advantage function): 描述的是最优动作 aa 的优势。
A∗(s,a)=Q∗(s,a)−V∗(s)A∗(s,a)=Q∗(s,a)−V∗(s)
定理:
V∗(s)=maxaQ∗(s,a)V∗(s)=amaxQ∗(s,a)
3.2目标
将优势函数两边最大化:
maxaA∗(s,a)=maxaQ∗(s,a)−V∗(s)=V∗(s)−V∗(s)=0amaxA∗(s,a)=amaxQ∗(s,a)−V∗(s)=V∗(s)−V∗(s)=0
故优势函数可以变形为:
Q∗(s,a)=A∗(s,a)+V∗(s)−maxaA∗(s,a)Q∗(s,a)=A∗(s,a)+V∗(s)−amaxA∗(s,a)
Note
dueling network就是对上式目标 Q∗(s,a)Q∗(s,a) 进行近似
4.网络结构
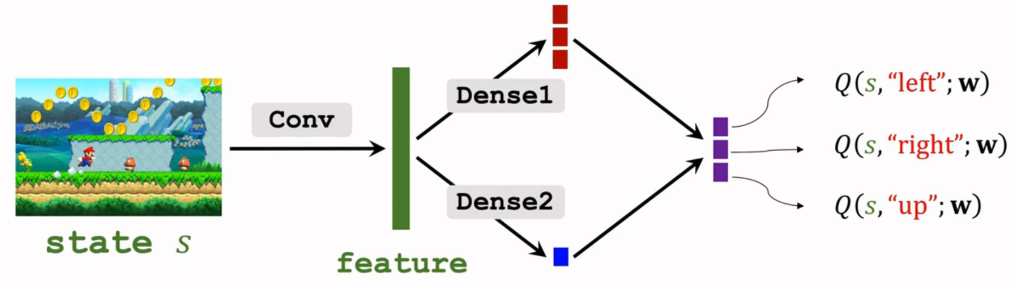
- 对 A∗(s,a)A∗(s,a) 与 V∗(s)V∗(s) 分别采用神经网络进行近似
Dense1:近似 A∗(s,a)A∗(s,a),即 A(s,a;wA)A(s,a;wA)Dense2:近似 V∗(s)V∗(s),即 V(s;wV)V(s;wV)
- 将系数合并:w=[wA,wV]w=[wA,wV]
- 目标就为:Q(s,a;w)=A(s,a;wA)+V(s;wV)−maxaA(s,a;wA)Q(s,a;w)=A(s,a;wA)+V(s;wV)−amaxA(s,a;wA)
- 系数更新方法与 DQN 一样
Tip
meanaA(s,a;wA)meanaA(s,a;wA) 的效果可能比 maxaA(s,a;wA)maxaA(s,a;wA) 好
蒙特卡洛
1.1计算π
1.1采样法
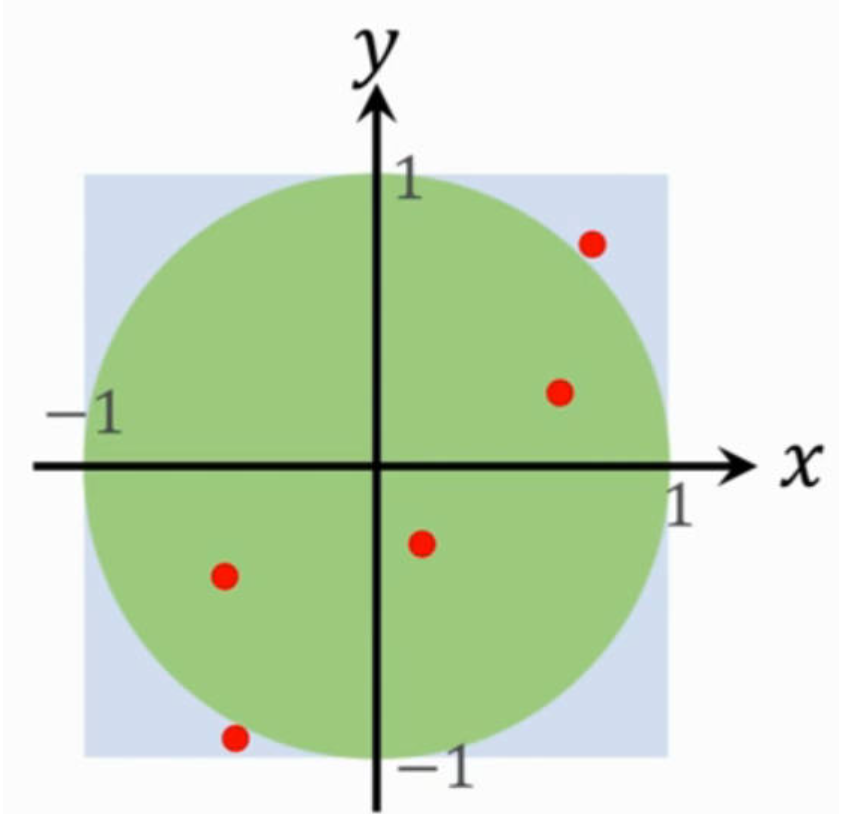
从图中可知:矩形的面积为 Ar=4Ar=4,圆的面积为 Ac=πAc=π。现在在矩形框内随机的抽取采样点(均匀抽样),那么采样点位于圆内的概率就为 p=AcAr=π4p=ArAc=4π。
步骤:
- 采样
m个点,有n个点在圆内 - ππ值就是:π≈4nmπ≈m4n
- 误差精度为:∣4nm−π∣=O(1m)∣m4n−π∣=O(m1)
1.2 buffon 针问题

所有的针都一摸一样,针与纸相交的概率就为 P=2lπdP=πd2l。这样根据monte carlo就计算 ππ。
2.计算定积分
问题: 计算下列定积分的值
I=∫abf(x) dxI=∫abf(x) dx
定积分的定义:
I=limn→∞∑i=0nf(a+i∗b−an)b−anI=n→∞limi=0∑nf(a+i∗nb−a)nb−a
近似计算:
- 在 [a,b][a,b] 内随机采样 x1,x2,⋯ ,xnx1,x2,⋯,xn
- 根据定积分定义进行近似计算:I≈(b−a)1n∑i=1nf(xi)I≈(b−a)n1i=1∑nf(xi)
3.计算期望
期望定义: 试验中每次可能结果的概率乘以其结果的总和,反映随机变量平均取值的大小。p(x)p(x)代表概率密度函数。
E(f(X))=∫f(x)p(x) dxE(f(X))=∫f(x)p(x) dx
近似计算:
- 根据概率密度函数 p(x)p(x) 随机采样 x1,x2,⋯ ,xnx1,x2,⋯,xn
- 根据定积分定义进行近似计算:E(f(X))≈1n∑i=1nf(xi)E(f(X))≈n1i=1∑nf(xi)










Comments NOTHING